Этап 3 "Треугольник Паскаля"
Блез Паскаль - Жизненный Путь:
Треугольник Паскаля:
История Треугольника Паскаля, как ни странно, начинается задолго до рождения самого ученого. И в мире существует множество версий этого треугольника.
Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма.

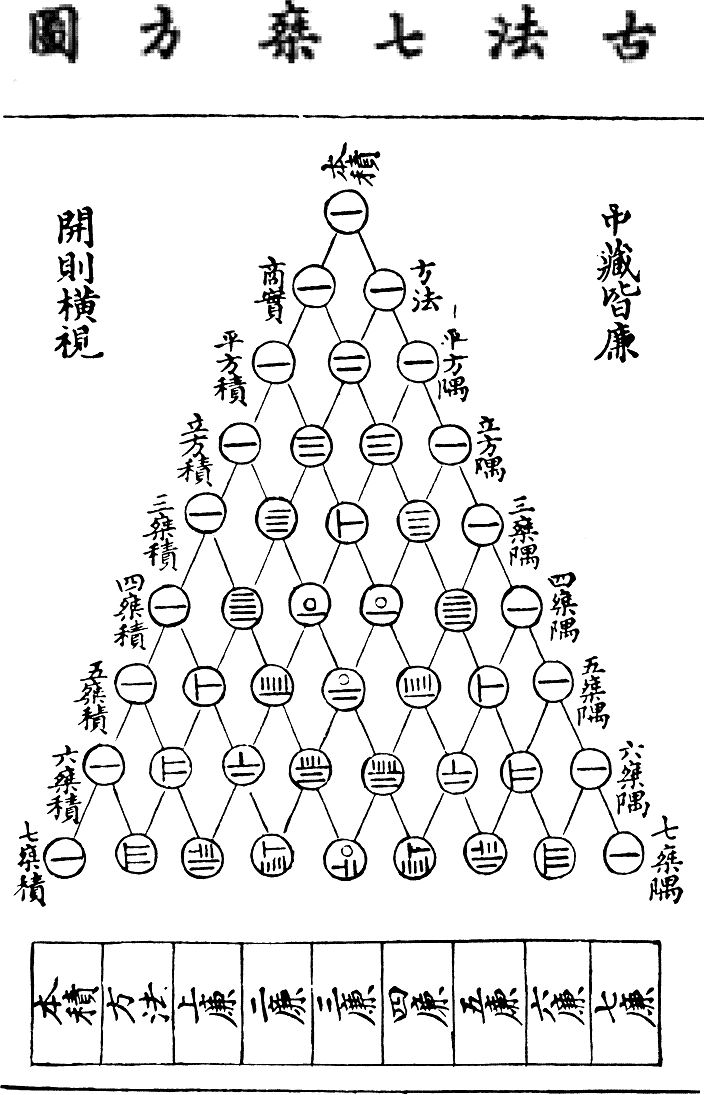
Считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя).
В Италии треугольник Паскаля иногда называют «треугольником Тартальи», поскольку Никколо Тарталья описал эту таблицу на сто лет раньше Паскаля.

На титульном листе учебника арифметики, написанн�ом в 1529 году Петром Апианом, астрономом из Ингольштадтского университета, также изображён треугольник Паскаля.
Треугольник Паскаля (арифметический треугольник) — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.

Свойства треугольника:
Биномиальные коэффициенты читаются как «число сочетаний из n элементов по k».
-
Числа треугольника симметричны (равны) относительно вертикальной оси.
-
В строке с номером n (нумерация начинается с 0):
-
первое и последнее числа равны 1.
-
второе и предпоследнее числа равны n.
-
третье число равно треугольному числу , что также равно сумме номеров предшествующих строк.
-
четвёртое число является тетраэдрическим.
-
m-е число (при нумерации с 0) равно биномиальному коэффициенту .
-
-
Сумма чисел восходящей диагонали, начинающейся с первого элемента (n-1)-й строки, есть n-е число Фибоначчи:
-
Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.
-
Все числа в n-й строке, кроме единиц, делятся на число n тогда и только тогда, когда n является простым числом (следствие теоремы Люка).
-
Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3n, 3n+1, 3n+2, то первые две суммы будут равны, а третья на 1 меньше.
-
Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз.

